9.1 Standard scores

Download notebook Interact

Describing distributions

We have seen several examples of distributions.

We can describe distributions as having a center, and a spread.

In the mean as predictor, we saw that the mean is a useful measure of the center of a distribution.

What measure should we use for the spread?

Chronic kidney disease

We’re going to work with a data set that was collected to help doctors diagnose chronic kidney disease (CKD). Each row in the data set represents a single patient who was treated in the past and whose diagnosis is known. For each patient, we have a bunch of measurements from a blood test.

You will see more of this dataset soon.

If you are running on your laptop, you should download the ckd.csv file to the same directory as this notebook.

ckd_full = pd.read_csv('ckd.csv')
ckd_full.head()

	Age	Blood Pressure	Specific Gravity	Albumin	Sugar	Red Blood Cells	Pus Cell	Pus Cell clumps	Bacteria	Blood Glucose Random	...	Packed Cell Volume	White Blood Cell Count	Red Blood Cell Count	Hypertension	Diabetes Mellitus	Coronary Artery Disease	Appetite	Pedal Edema	Anemia	Class
0	48	70	1.005	4	0	normal	abnormal	present	notpresent	117	...	32	6700	3.9	yes	no	no	poor	yes	yes	1
1	53	90	1.020	2	0	abnormal	abnormal	present	notpresent	70	...	29	12100	3.7	yes	yes	no	poor	no	yes	1
2	63	70	1.010	3	0	abnormal	abnormal	present	notpresent	380	...	32	4500	3.8	yes	yes	no	poor	yes	no	1
3	68	80	1.010	3	2	normal	abnormal	present	present	157	...	16	11000	2.6	yes	yes	yes	poor	yes	no	1
4	61	80	1.015	2	0	abnormal	abnormal	notpresent	notpresent	173	...	24	9200	3.2	yes	yes	yes	poor	yes	yes	1

5 rows × 25 columns

We will use this dataset to get a couple of variables (columns) and therefore a couple of distributions.

Let’s start with the White Blood Cell Count, usually abbreviated as WBC.

wbc = ckd_full['White Blood Cell Count']
wbc.hist()
plt.title('White Blood Cell Count');

png

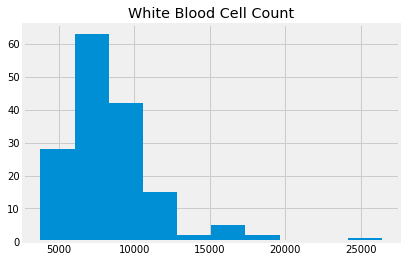
wbc.describe()

count      158.000000
mean      8475.949367
std       3126.880181
min       3800.000000
25%       6525.000000
50%       7800.000000
75%       9775.000000
max      26400.000000
Name: White Blood Cell Count, dtype: float64

Compare this to Hemoglobin concentrations:

hgb = ckd_full['Hemoglobin']
hgb.hist()
plt.title('Hemoglobin');

png

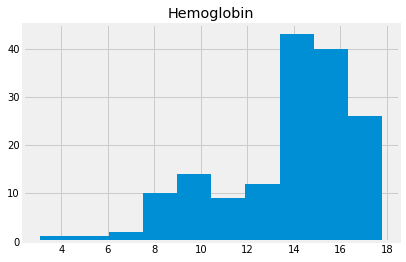
hgb.describe()

count    158.000000
mean      13.687342
std        2.882204
min        3.100000
25%       12.600000
50%       14.250000
75%       15.775000
max       17.800000
Name: Hemoglobin, dtype: float64

Notice that we can’t easily plot these two on the same axes, because their units are so different.

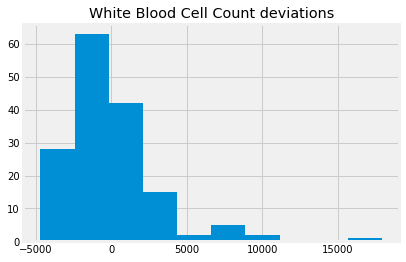
We could try and fix this by subtracting the mean, as a center value, so the values are now deviations from the mean.

wbc_deviations = wbc - np.mean(wbc)
wbc_deviations.hist()
plt.title('White Blood Cell Count deviations');

png

hgb_deviations = hgb - np.mean(hgb)
hgb_deviations.hist()
plt.title('Hemoglobin deviations');

png

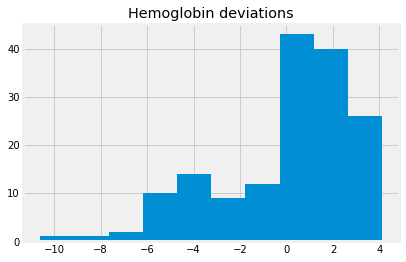
The deviations each have a mean very very close to zero, and therefore, they have the same center:

np.mean(wbc_deviations), np.mean(hgb_deviations)

(-1.8420145858692217e-13, 7.195369476051647e-16)

We still cannot plot them on the same axes, because the WBC values have a very different spread. They will completely dominate the x axis of the graph. We can’t reasonably compare the WBC deviations to the Hemoglobin deviations, because they have such different units.

We would like a measure of the spread of the distribution, so we can set the two distributions to have the same spread.

The standard deviation

In the mean as predictor section, we found that mean was the best value to use as a predictor, to minimize the sum of squared deviations.

Maybe we could get an idea of the typical squared deviation, as a measure of spread?

hgb_deviations[:10]

 -2.487342
 -4.187342
 -2.887342
 -8.087342
 -5.987342
 -3.887342
 -1.187342
 -3.687342
 -3.187342
 -3.887342
Name: Hemoglobin, dtype: float64

hgb_dev_sq = hgb_deviations ** 2
hgb_dev_sq[:10]

   6.186869
  17.533831
   8.336743
  65.405097
  35.848261
  15.111426
   1.409780
  13.596489
  10.159148
  15.111426
Name: Hemoglobin, dtype: float64

hgb_dev_sq.hist()
plt.title('HGB squared deviations')

Text(0.5, 1.0, 'HGB squared deviations')

png

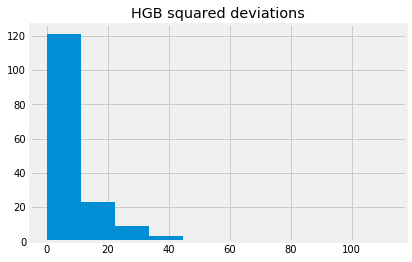
The center, or typical value, of this distribution, could be the mean.

hgb_dev_sq_mean = np.mean(hgb_dev_sq)
hgb_dev_sq_mean

8.254523313571543

This is the mean squared deviation. This is also called the variance. Numpy has a function to calculate that in one shot:

# The mean squared deviation is the variance
np.var(hgb)

8.254523313571543

The mean squared deviation is a good indicator of the typical squared deviation. What should we used for some measure of the typical devation?

We could take the square root of the mean squared deviation, like this:

np.sqrt(hgb_dev_sq_mean)

2.873068623192203

This is a measure of the spread of the distribution. It is a measure of the typical or average deviation.

It is also called the standard deviation.

np.std(hgb)

2.873068623192203

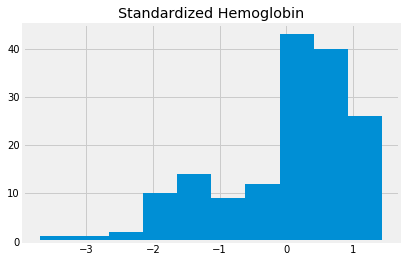
We can make our distribution have a standard center and a standard spread by dividing our mean-centered distribution, by the standard deviation. Then the distribution will have a standard deviation very close to 1.

This version of the distribution, with mean 0 and standard deviation of 1, is called the standardized distribution.

standardized_hgb = hgb_deviations / np.std(hgb)
standardized_hgb.hist()
plt.title('Standardized Hemoglobin')

Text(0.5, 1.0, 'Standardized Hemoglobin')

png

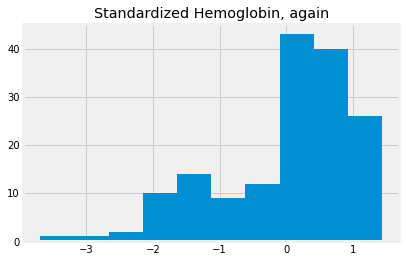
We can make a function to do this:

def standard_units(x):
    return (x - np.mean(x))/np.std(x)

std_hgb_again = standard_units(hgb)
std_hgb_again.hist()
plt.title('Standardized Hemoglobin, again')

Text(0.5, 1.0, 'Standardized Hemoglobin, again')

png

If we do the same to the WBC, we can compare values of the distributions:

std_wbc = standard_units(wbc)
std_wbc.hist()
plt.title('Standardized White Blood Cell Count')

Text(0.5, 1.0, 'Standardized White Blood Cell Count')

png

Every value in standardized units gives the deviation of the original value from its mean, in terms of the number of standard deviations.