5.1 Population and permutation

Download notebook Interact

A problem of populations

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# Fancy plots
plt.style.use('fivethirtyeight')

# Data frame library
import pandas as pd

We load the data:

# Load the data frame, and put it in the variable "audit_data"
audit_data = pd.read_table('audit_of_political_engagement_14_2017.tab')

Now get the ages for the Leavers and the Remainers:

# Drop rows where age is 0
good_data = audit_data.loc[audit_data['numage'] != 0]
# Get data frames for leavers and remainers
remain_ages = good_data[good_data['cut15'] == 1]['numage']
leave_ages = good_data[good_data['cut15'] == 2]['numage']

Show the age distributions for the two groups:

remain_ages.hist()
len(remain_ages)

png

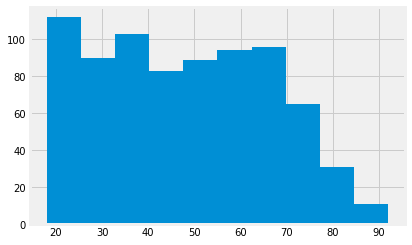
leave_ages.hist()
len(leave_ages)

png

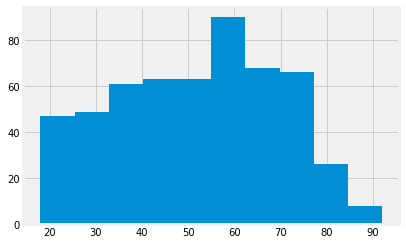
These certainly look like different distributions.

We might summarize the difference, by looking at the difference in means:

leave_mean = np.mean(leave_ages)
leave_mean

51.715341959334566

remain_mean = np.mean(remain_ages)
remain_mean

48.01550387596899

difference = leave_mean - remain_mean
difference

3.6998380833655773

The distributions do look different.

They have a mean difference of nearly 4 years.

Could this be due to sampling error?

If we took two random samples of 774 and 541 voters, from the same population, we would expect to see some difference, just by chance.

By chance means, because random samples vary.

What is the population, in this case?

It is not exactly the whole UK population, because the survey only sampled people who were eligible to vote.

It might not even be the whole UK population, who are eligible to vote. Perhaps the survey company got a not-representative range of ages, for some reason. We are not interested in that question, only the question of whether the Leave and Remain voters could come from the same population, where the population is, people selected by the survey company.

How do we find this population, to do our simulation?

Population by permutation

Here comes a nice trick. We can use the data that we already have, to simulate the effect of drawing lots of random samples, from the underlying population.

Let us assume that the Leave voters and the Remain voters are in fact samples from the same underlying population.

If that is the case, we can throw the Leave and Remain voters into one big pool of 774 + 541 == 1315 voters.

Then we can take split this new mixed sample into two groups, at random, one with 774 voters, and the other with 541. The new groups have a random mix of the original Leave and Remain voters. Then we calculate the difference in means between these two new, fake groups.

pooled = np.append(remain_ages, leave_ages)
pooled

array([37, 55, 37, ..., 20, 40, 31])

len(pooled)

We mix the two samples together, using np.random.shuffle. It works like this:

pets = np.array(['cat', 'dog', 'rabbit'])
pets

array(['cat', 'dog', 'rabbit'], dtype='<U6')

np.random.shuffle(pets)
pets

array(['dog', 'rabbit', 'cat'], dtype='<U6')

np.random.shuffle(pets)
pets

array(['rabbit', 'dog', 'cat'], dtype='<U6')

Now to mix up ages of the Leavers and Remainers:

np.random.shuffle(pooled)
pooled

array([38, 64, 22, ..., 39, 65, 19])

We split the newly mixed group into 774 simulated Remain voters and 541 simulated Leave voters, where each group is a random mix of the original Leave and Remain ages.

# The first 774 values
fake_remainers = pooled[:774]
# The rest
fake_leavers = pooled[774:]
len(fake_leavers)

Now we can calculate the mean difference. This is our first simulation:

fake_difference = np.mean(fake_leavers) - np.mean(fake_remainers)
fake_difference

-1.3059890049530196

That looks a lot smaller than the difference we saw. We want to keep doing this, to collect more simulations. We need to mix up the ages again, to give us new random samples of fake Remainers and fake Leavers.

np.random.shuffle(pooled)
fake_difference_2 = np.mean(pooled[:774]) - np.mean(pooled[774:])
fake_difference_2

-0.7007384162738148

We want to keep doing this, but copy / pasting seems like far too much work. We need - iteration.