Laws of probability¶

# Run this cell; do not change it.
import numpy as np
# Make printing of numbers a bit neater.
np.set_printoptions(precision=4, suppress=True)
import matplotlib.pyplot as plt
# Make the plots look more fancy.
plt.style.use('fivethirtyeight')

There are two important laws of probability that we will be using. Do not worry about the details of the text below for now, this page explains what the rules mean.

Multiplication rule: We get the probability of both of two events happening by multiplying the probability of the first event by the probability of the second event, given we know the first has occurred.
Addition rule: We get probability of either of two mutually exclusive events happening by adding the probability of the first event to the probability of the second event.

Multiplication rule¶

Remember our two boxes:

p_box4 = 0.3
p_box2 = 0.7

BOX4 has four red balls and one green ball. BOX2 has two red balls and three green balls.

box4 = np.repeat(['red', 'green'], [4, 1])
p_red_for_box4 = 0.8
box2 = np.repeat(['red', 'green'], [2, 3])
p_red_for_box2 = 0.4

Here we take 10000 boxes, and draw a ball from each box. We record which box we got and the color of the ball, for each trial.

n_iters = 10000
# The box for this trial.
box_types = np.repeat(['box?'], n_iters)
# The color of the ball we chose.
ball_colors = np.repeat(['green'], n_iters)
for i in np.arange(n_iters):
    # Choose a box number with a 30% chance of BOX4
    box_type = np.random.choice(['box4', 'box2'],
                                p=[p_box4, p_box2])
    # Choose a ball at random from the box.
    if box_type == 'box4':
        # Choose a ball at random from BOX4.
        ball_color = np.random.choice(box4)
    else:  # box 4
        # Choose a ball at random from BOX2.
        ball_color = np.random.choice(box2)
    # Store the results for each trial.
    box_types[i] = box_type
    ball_colors[i] = ball_color

As we expect from the law of large numbers, the proportions of BOX4 and BOX2 are very close to their initial probabilities.

print('Proportion of box4s',
      np.count_nonzero(box_types == 'box4') / n_iters)
print('Proportion of box2s',
      np.count_nonzero(box_types == 'box2') / n_iters)

Proportion of box4s 0.2859
Proportion of box2s 0.7141

Now let’s look at the proportion of all trials where we got both BOX4 and a red ball.

box4_and_red = np.logical_and(box_types == 'box4',
                              ball_colors == 'red')
print('Proportion of box4 then red',
      np.count_nonzero(box4_and_red) / n_iters)

Proportion of box4 then red 0.2286

Notice that this is very close to the result of multiplying: the probability of BOX4 by the probability of red, given we got BOX4.

p_box4 * p_red_for_box4

0.24

Here we look at the proportion of trials where we got both BOX2 and red.

box2_and_red = np.logical_and(box_types == 'box2',
                              ball_colors == 'red')
print('Proportion of box2 then red',
      np.count_nonzero(box2_and_red) / n_iters)

Proportion of box2 then red 0.2901

This is very close the probability of BOX2 times the probability of — red given we got BOX2.

p_box2 * p_red_for_box2

0.27999999999999997

Why?

Here is a Sankey diagram of that calculation:

If you follow the flow from right to left, you see that 30% of the trials will flow down the BOX4 arm, of which 80% will flow down the Red arm. 80% of 30% is (in proportions) 0.3 * 0.8 = 0.24.

Multiplication rule: To get the probability of both of two things happening, we multiply the probability of the first thing happening (e.g getting BOX4) by the probability of the second thing happening, once we know the first (here, the probability of getting red once we know we have BOX4).

Addition rule¶

Now imagine that, instead of two boxes, we have three boxes.

p_box4 = 0.3  # 30% chance of BOX4
p_box3 = 0.2  # 20% chance of BOX3
p_box2 = 0.5  # 50% chance of BOX2

The new box, BOX3, has three red balls and two green balls, giving a 60% chance we will draw a red ball from BOX3.

box3 = np.repeat(['red', 'green'], [3, 2])
p_red_for_box3 = 0.6

Here is a trial sampling lots of boxes, where we could get any one of boxes 4, 3 or 2.

boxes = np.random.choice(['box4', 'box3', 'box2'],
                          p=[p_box4, p_box3, p_box2],
                          size=10000)
prop4 = np.count_nonzero(boxes == 'box4') / 10000
print('Proportion of BOX4', prop4)
prop3 = np.count_nonzero(boxes == 'box3') / 10000
print('Proportion of BOX3', prop3)
prop2 = np.count_nonzero(boxes == 'box2') / 10000
print('Proportion of BOX2', prop2)

Proportion of BOX4 0.292
Proportion of BOX3 0.2013
Proportion of BOX2 0.5067

Now let’s think about the probability of getting either BOX4 or BOX3.

is_4_or_3 = np.logical_or(boxes == 'box4', boxes == 'box3')
prop4_or_3 = np.count_nonzero(is_4_or_3) / 10000
print('Proportion of BOX4 or BOX3', prop4_or_3)

Proportion of BOX4 or BOX3 0.4933

Notice that this has to be the same as:

prop4 + prop3

0.49329999999999996

It is also very close to:

p_box4 + p_box3

0.5

To see why, we do a Sankey (flow) diagram. Each box flows down one of three paths, the BOX4 path, the BOX3 path or the BOX2 path. In the long run, 30% of the boxes end up at the end of the BOX4 arm, 20% at the end of the BOX3 arm, and 50% at the end of BOX2 arm:

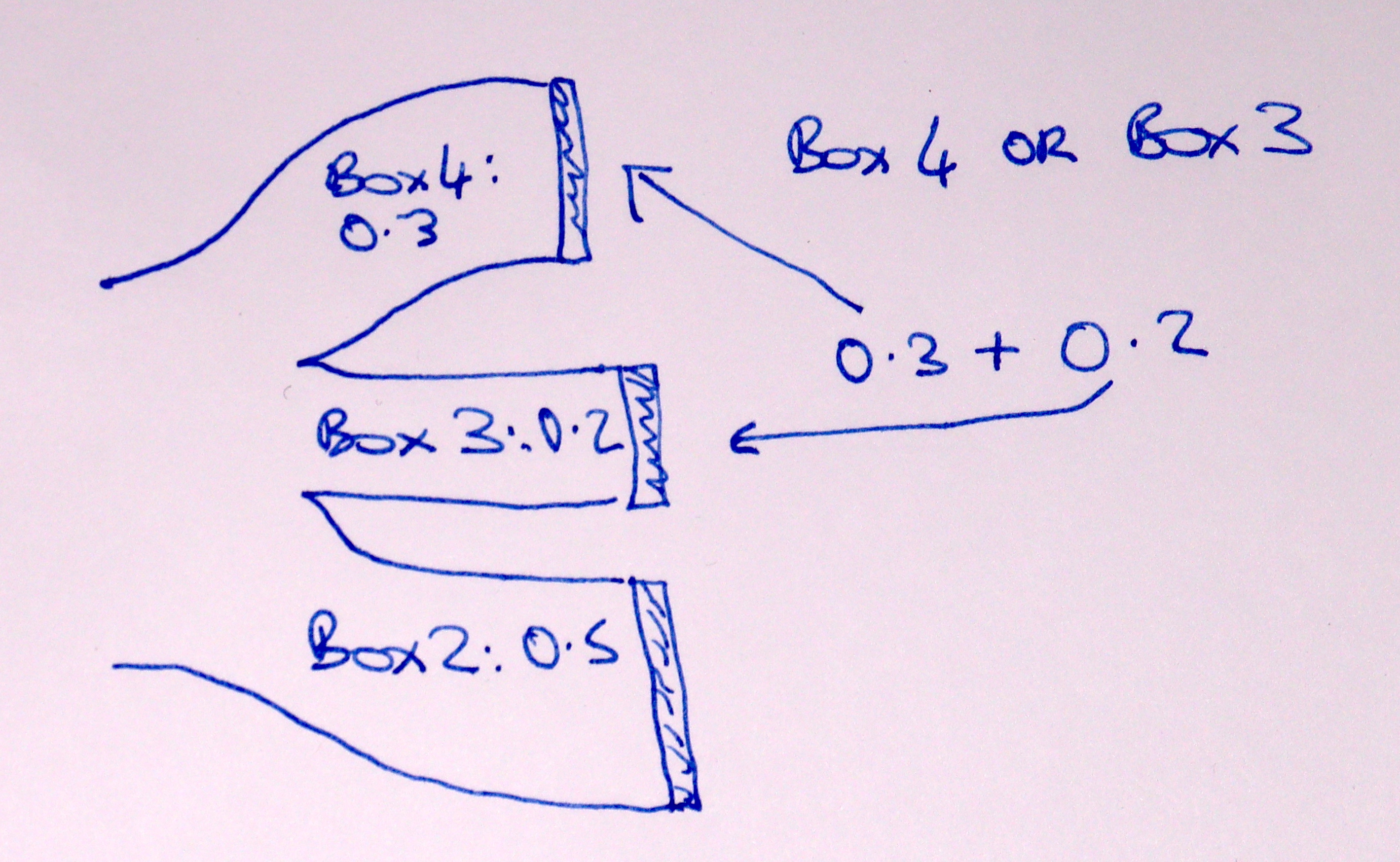
The proportion of BOX4 or BOX3 is just the number that go down either the BOX4 or BOX3 arm, and therefore:

print('Proportion of either BOX4 or BOX3', p_box4 + p_box3)

Proportion of either BOX4 or BOX3 0.5

Rule: To get the probability of either of two things happening, where those two things cannot happen at the same time, we add the probability of the first thing happening (e.g getting BOX4) to the probability of the second thing happening (e.g getting BOX3).

This rule only applies when the things that can happen are mutually exclusive. In our case, if the box is BOX4, it cannot also be BOX3. The fact that this is a BOX4 excludes the possibility it is BOX3 — and vice versa.

Coding for Data - 2020 edition

Laws of probability¶

Multiplication rule¶

Addition rule¶