Call expressions¶
Call expressions invoke functions, which are named operations. The name of the function appears first, followed by expressions in parentheses.
For example, abs is a function that returns the absolute value of the input
argument:
abs(-12)
12
round is a function that returns the input argument rounded to the nearest integer (counting number).
round(5 - 1.3)
4
max(2, 5, 4)
5
In this last example, the max function is called on three arguments: 2,
5, and 4. The value of each expression within parentheses is passed to the
function, and the function returns the final value of the full call
expression. You separate the expressions with commas: ,. The max function
can take any number of arguments and returns the maximum.
Many functions, like max can accept a variable number of arguments.
round is an example. If you call round with one argument, it returns the number rounded to the nearest integer, as you have already seen:
round(3.3333)
3
You can also call round with two arguments, where the first argument is the number you want to round, and the second argument is the number of decimal places you want to round to:
# Rounding to 0 decimal places.
round(3.3333, 0)
3.0
Notice that the result looks slightly different from the result of round(3.3333) above. We will get onto the these differences in the numbers section.
You can also round to - say - 2 decimal places, like this:
# Rounding to 2 decimal places.
round(3.3333, 2)
3.33
A few functions are available by default, such as abs and round, but most
functions that are built into the Python language are stored in a collection
of functions called a module. An import statement is used to provide
access to a module, such as math.
import math
math.sqrt(5)
2.23606797749979
Operators and call expressions can be used together in an expression. The
percent difference between two values is used to compare values for which
neither one is obviously initial or changed. For example, in 2014 Florida
farms produced 2.72 billion eggs while Iowa farms produced 16.25 billion eggs
1. The percent difference is 100 times the absolute value of the
difference between the values, divided by their average. In this case, the
difference is larger than the average, and so the percent difference is
greater than 100.
florida = 2.72
iowa = 16.25
100*abs(florida-iowa)/((florida+iowa)/2)
142.6462836056932
Learning how different functions behave is an important part of learning a
programming language. A Jupyter notebook can assist in remembering the names
and effects of different functions. When editing a code cell, press the tab
key after typing the beginning of a name to bring up a list of ways to
complete that name. For example, press tab after math. to see all of the
functions available in the math module. Typing will narrow down the list of
options. To learn more about a function, place a ? after its name. For
example, typing math.sin? will bring up a description of the sin
function in the math module. Try it now. You should get something like
this:
sqrt(x)
Return the square root of x.
The list of Python’s built-in
functions is quite long and
includes many functions that are never needed in data science applications.
The list of mathematical functions in the math
module is similarly long. This
text will introduce the most important functions in context, rather than
expecting the reader to memorize or understand these lists.
Example¶
In 1869, a French civil engineer named Charles Joseph Minard created what is still considered one of the greatest graphs of all time. It shows the decimation of Napoleon’s army during its retreat from Moscow. In 1812, Napoleon had set out to conquer Russia, with over 350,000 men in his army. They did reach Moscow but were plagued by losses along the way. The Russian army kept retreating farther and farther into Russia, deliberately burning fields and destroying villages as it retreated. This left the French army without food or shelter as the brutal Russian winter began to set in. The French army turned back without a decisive victory in Moscow. The weather got colder and more men died. Fewer than 10,000 returned.

The graph is drawn over a map of eastern Europe. It starts at the Polish-Russian border at the left end. The light brown band represents Napoleon’s army marching towards Moscow, and the black band represents the army returning. At each point of the graph, the width of the band is proportional to the number of soldiers in the army. At the bottom of the graph, Minard includes the temperatures on the return journey.
Notice how narrow the black band becomes as the army heads back. The crossing of the Berezina river was particularly devastating; can you spot it on the graph?
The graph is remarkable for its simplicity and power. In a single graph, Minard shows six variables:
the number of soldiers
the direction of the march
the latitude and longitude of location
the temperature on the return journey
the location on specific dates in November and December
Tufte says that Minard’s graph is “probably the best statistical graphic ever drawn.”
Here is a subset of Minard’s data, adapted from The Grammar of Graphics by Leland Wilkinson.
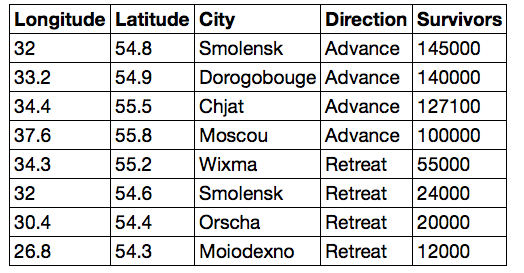
Each row of the column represents the state of the army in a particular location. The columns show the longitude and latitude in degrees, the name of the location, whether the army was advancing or in retreat, and an estimate of the number of men.
In this table the biggest change in the number of men between two consecutive locations is when the retreat begins at Moscow, as is the biggest percentage change.
moscou = 100000
wixma = 55000
wixma - moscou
-45000
(wixma - moscou)/moscou
-0.45
That’s a 45% drop in the number of men in the fighting at Moscow. In other words, almost half of Napoleon’s men who made it into Moscow didn’t get very much farther.
As you can see in the graph, Moiodexno is pretty close to Kowno where the army started out. Fewer than 10% of the men who marched into Smolensk during the advance made it as far as Moiodexno on the way back.
smolensk_A = 145000
moiodexno = 12000
(moiodexno - smolensk_A)/smolensk_A
-0.9172413793103448
Yes, you could do these calculations by just using the numbers without names. But the names make it much easier to read the code and interpret the results.
It is worth noting that bigger absolute changes don’t always correspond to bigger percentage changes.
The absolute loss from Smolensk to Dorogobouge during the advance was 5,000 men, whereas the corresponding loss from Smolensk to Orscha during the retreat was smaller, at 4,000 men.
However, the percent change was much larger between Smolensk and Orscha because the total number of men in Smolensk was much smaller during the retreat.
dorogobouge = 140000
smolensk_R = 24000
orscha = 20000
abs(dorogobouge - smolensk_A)
5000
abs(dorogobouge - smolensk_A)/smolensk_A
0.034482758620689655
abs(orscha - smolensk_R)
4000
abs(orscha - smolensk_R)/smolensk_R
0.16666666666666666
Note
This page has content from the Calls notebook of an older version of the UC Berkeley data science course. See the Berkeley course section of the license file.
