\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)

Formula for rotating a vector in 2D

Let’s say we have a point \((x_1, y_1)\). The point also defines the vector \((x_1, y_1)\).

The vector \((x_1, y_1)\) has length \(L\).

We rotate this vector anticlockwise around the origin by \(\beta\) degrees.

The rotated vector has coordinates \((x_2, y_2)\)

The rotated vector must also have length \(L\).

Theorem

\[\begin{split}x_2 = \cos \beta x_1 - \sin \beta y_1 \\ y_2 = \sin \beta x_1 + \cos \beta y_1\end{split}\]

See: wikipedia on rotation matrices.

Preliminaries

Call the angle between \((x_1, y_1)\) and the x-axis : \(\alpha\). Then:

(1)\[\begin{split}x_1 = L \cos(\alpha) \\ y_1 = L \sin(\alpha)\end{split}\]

We rotate \((x_1, y_1)\) by angle \(\beta\) to get \((x_2, y_2)\). So the angle between \((x_2, y_2)\) and the x-axis is \(\alpha + \beta\):

(2)\[\begin{split}x_2 = L \cos(\alpha + \beta) \\ y_2 = L \sin(\alpha + \beta)\end{split}\]

Proof by the angle sum rule

If you are happy with The angle sum rule proof, then we are most of the way there.

The angle sum rule gives us:

\[\begin{split}\cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta\end{split}\]

So, substituting from equations (1), (2):

\[\begin{split}L \cos(\alpha + \beta) = L \cos \alpha \cos \beta - L \sin \alpha \sin \beta \implies \\ x_2 = x_1 \cos \beta - y_1 \sin \beta \\\end{split}\]

We do the matching substitutions into \(\sin(\alpha + \beta)\) to get \(y_2\).

\(\blacksquare\)

Proof by long-hand variant of angle sum proof

This section doesn’t assume the angle sum rule, but uses a version of the angle-sum proof to prove the rotation formulae.

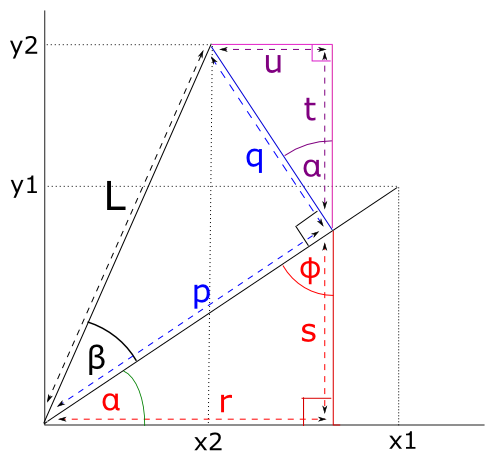
We can see from the picture that:

\[ \begin{align}\begin{aligned}x_2 = r - u\\y_2 = t + s\end{aligned}\end{align} \]

We are going to use some basic trigonometry to get the lengths of \(r, u, t, s\).

Because the angles in a triangle sum to 180 degrees, \(\phi\) on the picture is \(90 - \alpha\) and therefore the angle between lines \(q, t\) is also \(\alpha\).

Remembering the definitions of \(\cos\) and \(\sin\):

\[ \begin{align}\begin{aligned}\cos\theta = \frac{A}{H} \implies A = \cos \theta H\\\sin\theta = \frac{O}{H} \implies O = \sin \theta H\end{aligned}\end{align} \]

Thus:

\[ \begin{align}\begin{aligned}x_1 = \cos \alpha L\\y_1 = \sin \alpha L\\p = \cos \beta L\\q = \sin \beta L\\r = \cos \alpha p = \cos \alpha \cos \beta L = \cos \beta x_1\\s = \sin \alpha p = \sin \alpha \cos \beta L = \cos \beta y_1\\t = \cos \alpha q = \cos \alpha \sin \beta L = \sin \beta x_1\\u = \sin \alpha q = \sin \alpha \sin \beta L = \sin \beta y_1\end{aligned}\end{align} \]

So:

\[ \begin{align}\begin{aligned}x_2 = r - u = \cos \beta x_1 - \sin \beta y_1\\y_2 = t + s = \sin \beta x_1 + \cos \beta y_1\end{aligned}\end{align} \]

\(\blacksquare\).