\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)
Linear interpolation¶
See: wikipedia on linear interpolation.
Let us say that we have two known points \(x_1, y_1\) and \(x_2, y_2\).
Now we want to estimate what \(y\) value we would get for some \(x\) value that is between \(x_1\) and \(x_2\). Call this \(y\) value estimate — an interpolated value.
Two simple methods for choosing \(y\) come to mind. The first is see whether \(x\) is closer to \(x_1\) or to \(x_2\). If \(x\) is closer to \(x_1\) then we use \(y_1\) as the estimate, otherwise we use \(y_2\). This is called nearest neighbor interpolation.
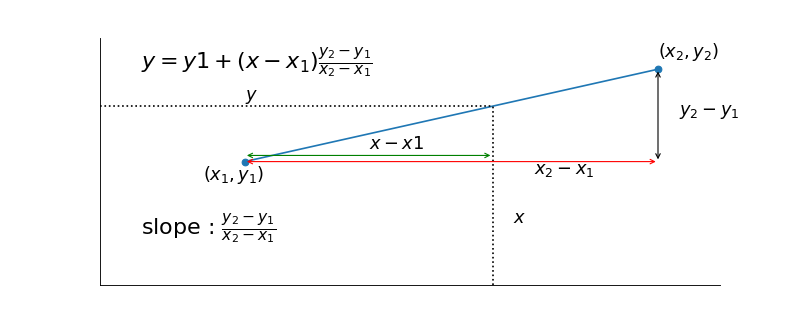
The second is to draw a straight line between \(x_1, y_1\) and \(x_2, y_2\). We look to see the \(y\) value on the line for our chosen \(x\). This is linear interpolation.
It is possible to show that the formula of the line between \(x_1, y_1\) and \(x_2, y_2\) is: