Gimbal lock

See also: http://en.wikipedia.org/wiki/Gimbal_lock

Euler angles have a major deficiency, and that is, that it is possible, in some rotation sequences, to reach a situation where two of the three Euler angles cause rotation around the same axis of the object. In the case below, rotation around the \(x\) axis becomes indistinguishable in its effect from rotation around the \(z\) axis, so the \(z\) and \(x\) axis angles collapse into one transformation, and the rotation reduces from three degrees of freedom to two.

Example

Imagine that we are using the Euler angle convention of starting with a rotation around the \(x\) axis, followed by the \(y\) axis, followed by the \(z\) axis.

Here we see a Spitfire aircraft, flying across the screen. The \(x\) axis is left to right (tail to nose), the \(y\) axis is from the left wing tip to the right wing tip (going away from the screen), and the \(z\) axis is from bottom to top:

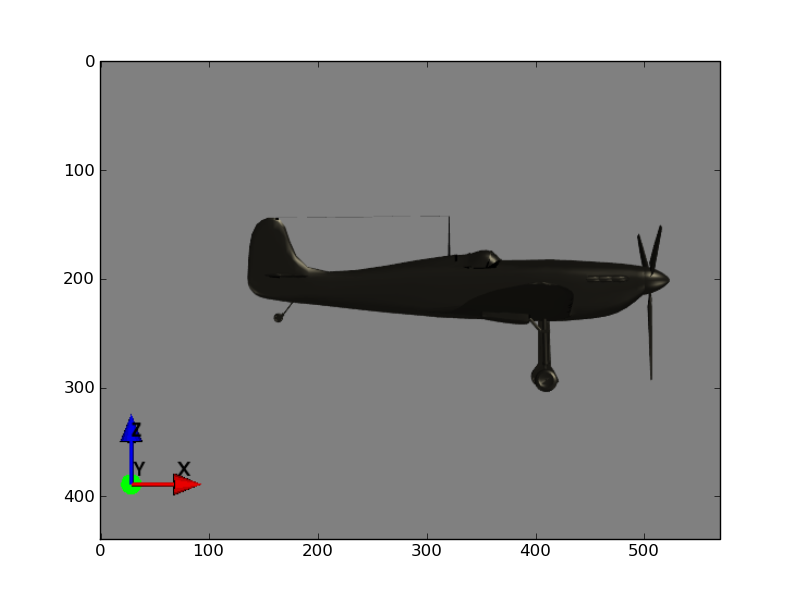
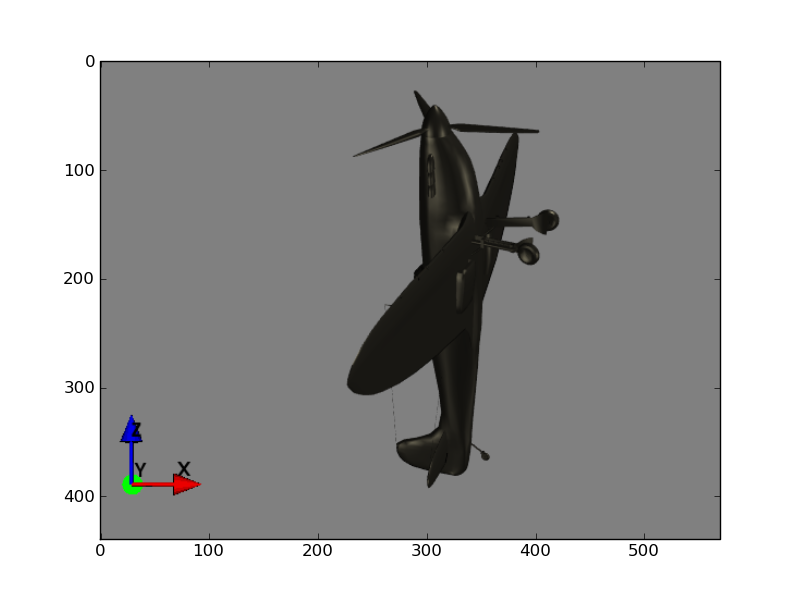
We want to rotate the aircraft to look something like this:

We might start by doing an x rotation, making a slight roll with the left wing tilting down (rotation about \(x\)) like this:

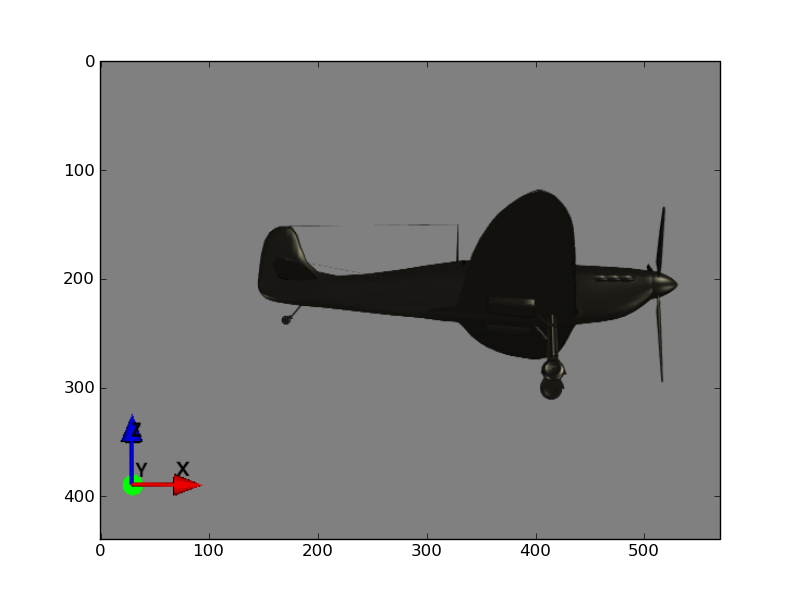
Let’s say that the x rotation is -0.2 radians.

Then we do a pitch so we are pointing straight up (rotation around \(y\) axis). This is a rotation by \(-\pi/2\) radians.

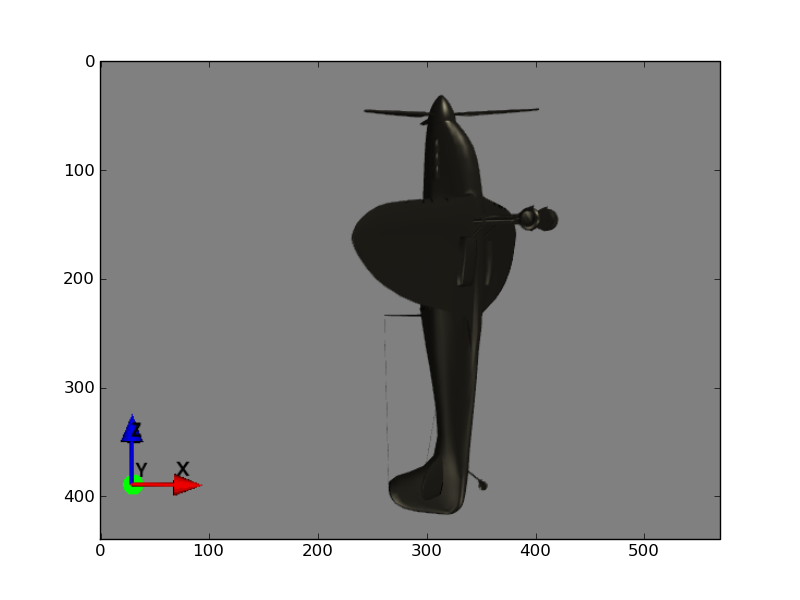
To get to our desired position from here, we need to do a turn of something like 0.2 radians of the nose towards the viewer (and the tail away from the viewer). All we have left is our z rotation (rotation around the \(z\) axis. Unfortunately, the current result of a rotation around the \(z\) axis has now become the same as a previous rotation around the \(x\) axis. To see this, look at the result of the rotation around the \(y\) axis. Notice that the \(x\) axis, as was, is now aligned with the \(z\) axis, as it is now. Rotating around the \(z\) axis will have exactly the same effect as adding an extra rotation around the \(x\) axis at the beginning. That means that, when there is a \(y\) axis rotation that rotates the \(x\) axis onto the \(z\) axis (a rotation of \(\pm\pi/2\) around the \(y\) axis) - the \(x\) and \(y\) axes are “locked” together.

This does not mean that we cannot do the rotations we need, only that we can’t do them by starting with the most obvious x and y rotations. In fact what we will have to do is first rotate around x by \(\pi/2 - 0.2\) radians, then do a y rotation of \(-\pi/2 + 0.2\) radians, and finally a z rotation of \(-\pi/2\) radians. See the code below for the details.

Mathematics of gimbal lock

See transforms3d.derivations.eulerangles.

We see gimbal lock for this type of Euler axis convention, when \(\cos(\beta) = 0\), where \(\beta\) is the angle of rotation around the \(y\) axis. By “this type of convention” we mean using rotation around all 3 of the \(x\), \(y\) and \(z\) axes, rather than using the same axis twice - e.g. the physics convention of \(z\) followed by \(x\) followed by \(z\) axis rotation (the physics convention has different properties to its gimbal lock).

We can show how gimbal lock works by creating a rotation matrix for the three component rotations. Recall that, for a rotation of \(\alpha\) radians around \(x\), followed by a rotation \(\beta\) around \(y\), followed by rotation \(\gamma\) around \(z\), the rotation matrix \(R\) is:

\[\begin{split}R = \left[\begin{matrix}\cos{\left (\beta \right )} \cos{\left (\gamma \right )} & \sin{\left (\alpha \right )} \sin{\left (\beta \right )} \cos{\left (\gamma \right )} - \sin{\left (\gamma \right )} \cos{\left (\alpha \right )} & \sin{\left (\alpha \right )} \sin{\left (\gamma \right )} + \sin{\left (\beta \right )} \cos{\left (\alpha \right )} \cos{\left (\gamma \right )}\\\sin{\left (\gamma \right )} \cos{\left (\beta \right )} & \sin{\left (\alpha \right )} \sin{\left (\beta \right )} \sin{\left (\gamma \right )} + \cos{\left (\alpha \right )} \cos{\left (\gamma \right )} & - \sin{\left (\alpha \right )} \cos{\left (\gamma \right )} + \sin{\left (\beta \right )} \sin{\left (\gamma \right )} \cos{\left (\alpha \right )}\\- \sin{\left (\beta \right )} & \sin{\left (\alpha \right )} \cos{\left (\beta \right )} & \cos{\left (\alpha \right )} \cos{\left (\beta \right )}\end{matrix}\right]\end{split}\]

In our case the y rotation \(\beta = -\pi / 2, \cos(\beta) = 0, \sin(\beta) = -1\):

\[\begin{split}R = \left[\begin{matrix}0 & - \sin{\left (\alpha \right )} \cos{\left (\gamma \right )} - \sin{\left (\gamma \right )} \cos{\left (\alpha \right )} & \sin{\left (\alpha \right )} \sin{\left (\gamma \right )} - \cos{\left (\alpha \right )} \cos{\left (\gamma \right )}\\0 & - \sin{\left (\alpha \right )} \sin{\left (\gamma \right )} + \cos{\left (\alpha \right )} \cos{\left (\gamma \right )} & - \sin{\left (\alpha \right )} \cos{\left (\gamma \right )} - \sin{\left (\gamma \right )} \cos{\left (\alpha \right )}\\1 & 0 & 0\end{matrix}\right]\end{split}\]

From the angle sum and difference identities (see also geometric proof, Mathworld treatment) we remind ourselves that, for any two angles \(\alpha\) and \(\beta\):

\[ \begin{align}\begin{aligned}\sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \,\\\cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta\end{aligned}\end{align} \]

We can rewrite \(R\) as:

\[\begin{split}R = \left[\begin{matrix}0 & - W_{1} & - W_{2}\\0 & W_{2} & - W_{1}\\1 & 0 & 0\end{matrix}\right]\end{split}\]

where:

\[ \begin{align}\begin{aligned}W_1 = \sin{\left (\alpha \right )} \cos{\left (\gamma \right )} + \sin{\left (\gamma \right )} \cos{\left (\alpha \right )} = \sin(\alpha + \gamma) \,\\W_2 = - \sin{\left (\alpha \right )} \sin{\left (\gamma \right )} + \cos{\left (\alpha \right )} \cos{\left (\gamma \right )} = \cos(\alpha + \gamma)\end{aligned}\end{align} \]

We immediately see that \(\alpha\) and \(\gamma\) are going to lead to the same transformations - the mathematical expression of the observation on the spitfire above, that rotation around the \(x\) axis is equivalent to rotation about the \(z\) axis.

It’s easy to do the same set of reductions for the case where \(\sin(\beta) = 1\); see http://www.gregslabaugh.name/publications/euler.pdf.

The example in code

Here is what our gimbal lock looks like in code:

>>> import numpy as np
>>> np.set_printoptions(precision=3, suppress=True)  # neat printing
>>> from transforms3d.euler import euler2mat, mat2euler
>>> x_angle = -0.2
>>> y_angle = -np.pi / 2
>>> z_angle = -0.2
>>> R = euler2mat(x_angle, y_angle, z_angle, 'sxyz')
>>> R
array([[ 0.   ,  0.389, -0.921],
       [-0.   ,  0.921,  0.389],
       [ 1.   , -0.   ,  0.   ]])

This isn’t the transformation we actually want because of the gimbal lock. The gimbal lock means that x_angle and z_angle result in rotations about the same axis of the object. So, we can add something to the x_angle and subtract the same value from z_angle to get the same result:

>>> R = euler2mat(x_angle + 0.1, y_angle, z_angle - 0.1, 'sxyz')
>>> R
array([[ 0.   ,  0.389, -0.921],
       [-0.   ,  0.921,  0.389],
       [ 1.   , -0.   ,  0.   ]])

In fact, we could omit the z rotation entirely and put all the rotation into the original x axis rotation and still get the same rotation matrix:

>>> R_dash = euler2mat(x_angle + z_angle, y_angle, 0, 'sxyz')
>>> np.allclose(R, R_dash)
True

So, there is no future in doing our transformations starting with this x and y rotation, if we are rotating with this axis order. We can get the transformation we actually want by doing the rotations in the order x, then z then y, like this:

>>> R = euler2mat(x_angle, z_angle, y_angle, 'sxzy')
>>> R
array([[ 0.   ,  0.199, -0.98 ],
       [-0.199,  0.961,  0.195],
       [ 0.98 ,  0.195,  0.039]])

We can get this same transformation using our original x, y, z rotation order, but using different rotation angles:

>>> x_dash, y_dash, z_dash = mat2euler(R, 'sxyz')
>>> np.array((x_dash, y_dash, z_dash))  # np.array for print neatness
array([ 1.371, -1.371, -1.571])
>>> R = euler2mat(x_dash, y_dash, z_dash, 'sxyz')
>>> R
array([[ 0.   ,  0.199, -0.98 ],
       [-0.199,  0.961,  0.195],
       [ 0.98 ,  0.195,  0.039]])