\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)

Paired permutation test

• Download this page as a Jupyter notebook (no outputs).

Test the null hypothesis that the values for two variables are interchangeable.

See Attitudes to animal research.

>>> import random

>>> def mean(a_list):
...     return sum(a_list) / len(a_list)

>>> def mean_with_swap(list_1, list_2):
...     # Make new lists where some are swapped
...     new_list_1 = []
...     new_list_2 = []
...     for i in range(len(list_1)):
...         if random.random() >= 0.5:
...             # Don't swap
...             value_1 = list_1[i]
...             value_2 = list_2[i]
...         else:
...             # Swap
...             value_2 = list_1[i]
...             value_1 = list_2[i]
...         new_list_1.append(value_1)
...         new_list_2.append(value_2)
...     return mean(new_list_1) - mean(new_list_2)

>>> def paired_permute(variable_1, variable_2):
...     n_samples = 10000
...     sampled_means = []
...     observed = mean(variable_1) - mean(variable_2)
...     for i in range(n_samples):
...         one_trial = mean_with_swap(variable_1, variable_2)
...         sampled_means.append(one_trial)
...     return observed, sampled_means

In action on the animal attitude data:

>>> import pandas as pd
>>> questions = pd.read_csv('animal_questions.csv')
>>> trust_uni = list(questions['trust_uni'])
>>> trust_protectors = list(questions['trust_protectors'])
>>> observed, samples = paired_permute(trust_uni, trust_protectors)
>>> observed
0.017223910840932111

Hint

If running in the IPython console, consider running %matplotlib to enable interactive plots. If running in the Jupyter Notebook, use %matplotlib inline.

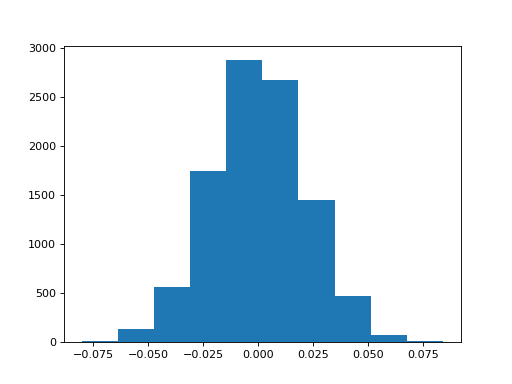
>>> import matplotlib.pyplot as plt
>>> plt.hist(samples)
(...)

(png, hires.png, pdf)